Generative Adversarial Networks:Part I

A brief Introduction to GAN's

Posted on April 30, 2017

In this tutorial, we will cover:

  1. Brief introduction to Generative Models.
  2. What are GAN’s?
  3. Why and where to use GAN's?
  4. Project on how to use GAN's to generate MNIST data.

There are usually two types of Generative Modelling techniques:

  1. Density Estimation: where you take some points on a 1-D number line and fit a Gaussian (normal/bell shape) curve and fit a density function to them.

  2. Sample Generation: where you take a machine, observe some examples from a distribution and create some new examples from that distribution.

So, the first question arises that why should we study GAN's and more generally Generative Modelling?

  1. It has been found that Generative models prove to be great test of our ability to use high-dimensional complicated probability distribution.

  2. Generative models help us to simulate possible future or models before implementing them or simulate Reinforcement Learning techniques. This helps to make the system more robust as we train the agent in a simulated environment that's built entirely by the Generative models rather than making and feeding the environment by hand where there can be some loopholes.

  3. Generative models are easy to parallelize on a GPU and the cost for the mistakes is not that high as can be while creating environment by hand.

  4. Generative models can handle the missing data in a dataset more efficiently. It can learn and generate the missing data and even generate missing labels in the unlabeled data.

  5. Generative models are great for speech modelling, text to image, generating word embedding’s etc.

Now, you must be thinking that there are other generative models as well that do a good work, so why study GAN's specifically? GAN's have some special properties due to which they are better than others as a generative model.

  1. Firstly, the GAN's use a latent code as compared to other adversarial networks like PixelCNN.

  2. GAN's are asymptotically consistent unlike the Variational Autoencoders.

  3. Also, to make a GAN, no Markov Chains are required.

  4. GAN's are also often regarded as producing the best samples in the output as compared to other conventional approaches.

    5. For example, in a paper by Lotter et al, 2016, it shows that when we want to generate the next video frame, using the conventional approaches like using the Mean Squared Error (MSE) leads to a blurry image at the output because that output is formed by averaging over all the previous frames.

    In contrast to MSE, using GAN's use adversarial loss technique to generate the image and hence the image obtained at the output is crisp.

  5. GAN's or Generative Adversarial Networks take a collection of training examples and forms some representation of probability distribution. Like Variational Autoencoders are good at getting a high likelihood, GAN's can generate real life examples.

So, let's dive into the world of GAN's.

GAN or Generative Adversarial Networks have recently been of great interests among the Machine Learning and Deep Learning community. Recently Yann LeCun, Director of AI Research at Facebook and Professor at NYU, said that "The most important and potentially upcoming breakthroughs in Deep Learning, in my opinion, is adversarial training (also called GAN for Generative Adversarial Networks)".

The concept of GAN's was first introduced by Dr. Ian Goodfellow, a PhD from University of Montreal and currently a researcher at OpenAI.

GAN's or Generative Adversarial Networks is a class of Neural Networks which allows the network to learn to generate data with the same internal structures as input/training data.

A basic GAN has two main parts/networks:

  1. Discriminator
  2. Generator

Discriminator (D):

As the name suggests, the goal of a discriminator is to discriminate between the real and the fake data. It is more like a binary classifier that classifies the inputs as real or from the training data and fake or generated data.

It uses a neural network (or any other network) to learn the input functions from the data and hence during testing it can classify that whether the test data is from a training set i.e. the one it has seen earlier or the fake data.

Generator (G):

As the name suggests, the goal of the generator is to generate the data similar to some models from the training data.

So how does it actually work?

The input to the generator is a noise data which is almost equal to or smaller than the dimensions of the input data. The generator network also uses a neural network to generate an output data. This data is then sent to the discriminator which tells that whether the data generated is real or fake and if fake then how far is it from the original/real data.

This error is fed back into the neural network to learn the data representations. After some training, the generator is able to output the data that the discriminator classifies as real and the generator is able to fool the discriminator.

This process does not end at a single iteration. There can be thousands of iterations before the generator is able to produce data similar to the real data.

You can see the working of the generator as a Reinforcement Learning problem. When the discriminator classifies the generated image as fake, there is a negative reward that is awarded to the generator network. The generator network continuously tries to maximize the reward and minimize the error.

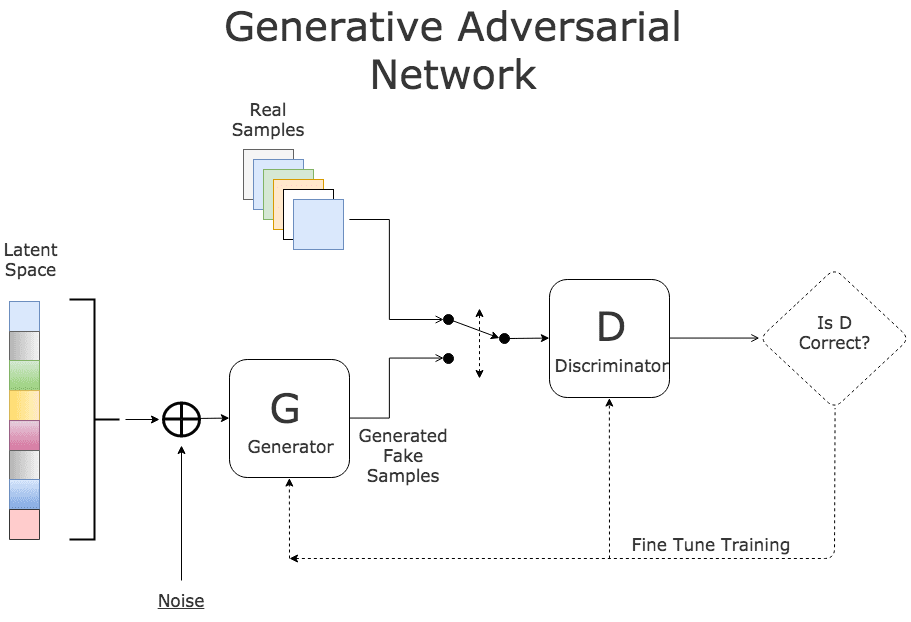
GAN Working:

The figure below shows and summarizes the working of the Discriminator and a Generator in a GAN:

  1. Firstly we take the training data and take a sample "x" from it. This data is input to a Discriminator which is essentially a Neural Network (or any other network). This network gets trained on the trainig data and hence, on the output the discriminator D(x) tries to classify each of the training samples as "1" i.e. real/original data.

  2. In case of a Generator, we input the data as random noise. The generator is also a Neural Network (or any other network) which generates an output data. This data is sent to the discriminator for classification.

  3. The Discriminator (D) tries to make the factor D(G(z)) as near to zero i.e. fake data detected whereas the Generator tries to make the factor D(G(z)) as near to "1" as possible i.e. the discriminator is fooled by the generator's output.

  4. Finally, at the end, both of thm settle down at a point called the saddle point. This point is where the Discriminator classifies the generated images as real rather than fake.

Mathematical Notations:

  1. Let us consider two random variables "x" and "y" where "x" represents the observed or the real data and "y" represents the target or generated data.

  2. Then, the joint distribution for x and y is given as P(x,y) where P(x,y) is the probability density over the two variables.

  3. A Discriminator evaluates the conditional probability P(y|x) i.e. probability of y given x. Ex. given the input vector of pixels from MNIST dataset, what is the probability that y = 1 i.e. the label of the pixel values is "1".

  4. On the other hand a Generator model allows us to evaluate the joint probability P(x,y).

  5. This shows that we can propose value pairs of the form (x,y) and do rejection sampling to obtain samples x and y from P(x,y) or in simple terms you can say that we can input a random number of form [0,1] and output a picture of a bird.

  6. In practice, the discriminator takes as input a set of random data which can be either real (x) or generated (G(z)) where "z" is the random noise data, and it produces the probability of the generator data being real (P(x)).

In other words, Discriminator (D) and Generator (G) play a two-player minimax game with value function V (G, D) as shown below:

where,

    D(x) represents the probability that "x" came from original data rather than generated data.
    D(G(z)) is the factor that the Discriminator wants to minimize and the Generator wants to maximize.

Now let’s have a look at the Algorithm that governs the minmax game that we discussed above.

As we can see from the algorithm given above, firstly the Discrimintaor is updated by ascending its stocastic gradient for "k" number of steps. For each "k" steps, the Generator Network is trained once.

The discriminator is optimized in order to increase the likelihood of giving a high probability to the real data and a low probability to the fake data.

The following equation, also the cost/loss equation for the Discriminator, is used to train the discriminator as shown below:

In the above equation, the aim of our optimizer is to maximize the first part of the above equation i.e. maximize(D(x)) and minimize the other term i.e. minimize(D(G(z)).
Why do we do this? Because we know that when we train the Discriminator, it tries to make the value of D(G(z)) near to "0" and the generator tries to make the value D(G(z)) near to "1".

Then we optimize the Generator as discussed in order to increase the probability of data being rated highly.

The following equation is used to train the Generator:

While optimizing for the generator, we want to maximize the term D(G(x)).

By alternating the gradient optimizations between the Generator and the Discriminator using the above given expressions on new batch of real and generated data each time, the GAN slowly starts converging and produces data that is as realistic as the network is capable of modelling.

We have been talking about the Discriminator a lot in the above discussion. So, how do we define an optimal discriminator.

For a fixed Generator, the optimal discriminator is given by the following ratio:

where,

    pdata is the training data distribution
    pg is the generative distribution

Estimating this ratio for D(x) using supervised learning is the key approximation mechanism used by the GAN's.

The training objective for a Discriminator is to maximize the log-likelihood for estimating the conditional probability P (Y = y|x), where Y indicates whether "x" comes from the original data or the generated data.

When the generated data becomes equal to the original data and the discriminator is not able to differentiate between the two data, the ratio of D(x) is equal to 0.5 at that time. At this time, we say that the generator has successfully fooled the discriminator. This point is called the Saddle Point.

Steps to Train the Generator and Discriminator:

The discriminator and generator are trained in an alternating fashion. Over time the discriminator learns ways to discriminate between the real data and the fake data. This helps making the generator more robust.

Also, note that some people also like to train these networks in a different way. In this approach, for each "n" number of iterations of the discriminator, we train the generator once, thereby making both the generator and the discriminator more robust.

The only drawback of this approach is that it takes a lot of time and iterations before the generator fools the discriminator. In more common terms, the generator and discriminator can be seen as playing a min-max game using a feed forward neural network.

Following are the steps used to train a GAN:

  1. Choose an optimization algorithms. ex. Adam
  2. Choose two minibatches and apply optimization to both of them. The two minibatches are one of training examples and the other of generated samples.
  3. One optional step is to run the optimization for "k" steps for one player, say, the Discriminator, for every single step of the Generator.

NOTE that the optimizer must be perfect else it can lead to underfitting. Also the dataset must be large else it can cause overfitting.

So, now we have reached the end of Part 1 of this tutorial. I hope I was able to clearly represent the working of GAN's.

For a deeper insight into GAN's watch this video and read these two papers: Paper 1 and Paper 2.

For Part 2 of this tutorial, click here

For more projects and code, follow me on Github

Please feel free to leave any comments, suggestions, corrections if any :)

comments powered by Disqus